面白い本です。世界中の「四角いモノ」を集めています。伝説から、ゲームから、建築から・・・。ムナーリさんの知識の広さがわかりますね。まだ「ググる」ことができない時代ですよ。
芸術家は、基本四角から始まります。らくがき帳も、キャンバスも四角です。四角は論理的思考、あるいは識字文化(本、これも四角)と相性がいいのかもしれません。四角にとらわれないで絵を描いた人(例えば子供の頃空き地で地面に落書きをしたなど)は感覚が違うのかもしれません。今では、遊び場(道路、公園など)も四角いですからね。家も部屋も基本的には四角い。四角いと安心するのか、四角に安心するように育てられたのか。「四角い思考」「四角い感覚」「四角い政治」なども定義できるかもしれません。
この本の中で、1:√nの長方形を描く方法が載っていました。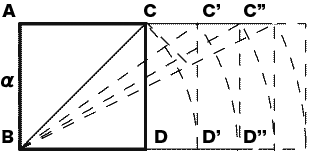
正方形ABCDのBCを半径とした円を書き、ADの延長との接点をD'とします。長方形ABC'D'の長辺の長さが√2となります。さらにBC'を半径とした円を描きADの延長との接点をD''とします。長方形ABC''D''の長編の長さは√3となります。
これは簡単に証明できます。ABの長さをα、n回目の図形をABC''D''とすると、BD''の長さは、√nα。ピタゴラスの定理から、
(BD'')の二乗 + (C''D'')の二乗 = (BC'')の二乗
√nα×√nα + α×α = n×α×α + α×α =(n+1)×α×α
よって、BD''=√(n+1)×α
です。
そこで問題ですが、図を見ると、長さの差分、DD'は次のD'D''より長い。ということは√nと√(n+1)との増分は、nが大きくなるにつれて小さくなるということです。では、底辺の長さはnが無限になると一定の値に近づくのでしょうか。もしそうなら、数学史に残る発見です。でも、答えはNoです。証明は省略。単純にnが一つ増えれば、BCを底辺とする正方形の面積がα×αづつ増えます。
では、√nと√(n+1)の差がだんだん小さくなっていくのはなぜでしょう。どうやらχのn乗の増分(nは正の数)はnが1の時は一定、n<1のときは減少、n>1のときは増加するようです。(誰か証明してください。)
更に思いついてたのですが、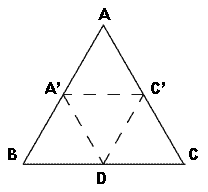
正三角形ABCの一辺の長さがαだとします。ABの中点、ACの中点を結ぶ線で折ると二つの山形ができます(BA'-A'D-DC'-C'C)。この長さは1/2αの長さが4本です。つまり、1/2α×4 = 2αです。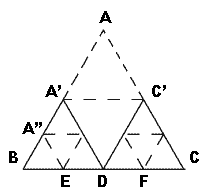
次に、この二つの山をその高さの半分でまたおります。すると8つの山ができます。この長さは1/4α×8です。これをn回繰り返します。この山の稜線は1/(2のn乗) × α × 2の(n-1)乗になります。これを無限に繰り返すとこの山は三角形の底辺に近づいていきませんか。でも、山の稜線の合計はいつまで経っても2 × αです。nには関係ありません。底辺の長さはα。同じにはなりません。
これは、三角を折るという行為、すなわち運動を表しているからです。そして、山形は「一であり多」「多であり一」、絶対的自己同一的矛盾、すなわち西田哲学です。(笑)
It's an interesting book. We collect "square things" from all over the world. From legends, games, architecture ... You can see the breadth of Munari's knowledge. It's an era when you can't "google" yet.
The artist starts with a basic square. Both the scribble book and the canvas are square. Squares may be a good match for logical thinking or literacy culture (books, also squares). People who draw pictures without being bound by squares (for example, when they were children, scribbled on the ground in a vacant lot) may have a different feeling. Playgrounds (roads, parks, etc.) are now square. Both the house and the room are basically square. Was it reassuring to be a square, or was it raised to be reassuring to be a square? It may be possible to define "square thinking," "square feeling," "square politics," and so on.
In this book, there was a way to draw a 1: √n rectangle.

Draw a circle with BC as the radius of the square ABCD, and let D'be the point of contact with the extension of AD. The length of the long side of the rectangle ABC'D'is √2. Furthermore, draw a circle with BC'as the radius and let D'' be the point of contact with the extension of AD. The length of the feature length of the rectangle ABC''D'' is √3.
This is easy to prove. If the length of AB is α and the nth figure is ABC''D'', the length of BD'' is √nα. From the Pythagorean theorem
(BD'') squared + (C''D'') squared = (BC'') squared
√nα × √nα + α × α = n × α × α + α × α = (n + 1) × α × α
Therefore, BD'' = √ (n + 1) × α
is.
So the problem is, looking at the figure, the difference in length, DD', is longer than the next D'D''. This means that the increment of √n and √ (n + 1) decreases as n increases. Then, does the length of the base approach a constant value when n becomes infinite? If so, it's a discovery in the history of mathematics. But the answer is no. Proof is omitted. If n is simply increased by one, the area of the square with BC as the base will increase by α × α.
So why is the difference between √n and √ (n + 1) getting smaller and smaller? Apparently, the increment of χ to the nth power (n is a positive number) is constant when n is 1, decreases when n <1, and increases when n> 1. (Please prove someone.)
I had an idea,

Suppose the length of one side of the equilateral triangle ABC is α. Fold it along the line connecting the midpoints of AB and AC to form two chevrons (BA'-A'D-DC'-C'C). This length is 1 / 2α with 4 lengths. That is, 1 / 2α × 4 = 2α.

Next, we straddle these two mountains at half their height. Then there will be 8 mountains. This length is 1/4 α x 8. Repeat this n times. The ridgeline of this mountain is 1 / (2 to the nth power) x α x 2 to the (n-1) power. If you repeat this infinitely, will this mountain approach the bottom of the triangle? However, the total of the mountain ridges is 2 x α forever. It has nothing to do with n. The length of the base is α. It will not be the same.
This is because it represents the act of folding a triangle, that is, movement. And Yamagata is "one and many" and "many and one", an absolute self-identical contradiction, that is, Nishida's philosophy. (Lol)
[出演者(プロフィール)]
ムナーリ,ブルーノ
1907年ミラノ生まれ。イタリアの前衛美術活動「未来派」に共鳴し、造形作品の発表を始める。またその傍ら、1930年代より、グラフィックデザイナー、アートディレクターとして本の編集や装丁を手がけ、戦後は、ダネーゼ社などのためのプロダクトデザインも多く手がける。1954年、55年、77年に、イタリアのデザイン賞「コンパッソ・ドーロ」を受賞。1940年代より制作を始めた、子どもの想像力を育てる実験的な絵本によって、絵本作家としても世界に知られており、1974年に、国際アンデルセン賞を受賞
阿部/雅世
1962年東京生まれ。建築家、デザイナー。法政大学工学部建築学科卒。イタリア・ドムスアカデミー工業デザイン科マスター修了。「五感に響くデザイン」を研究課題とし、ICFF2000Editor’s Award、A&W Mentor Award 2006ほか、建築、デザイン、素材研究など、幅広い分野で国際デザイン賞受賞。04‐07年国立ベルリン芸術大学客員教授、07‐09年国立エストニア芸術大学教授を務め、世界各地で子どもやプロのデザイナーを対象としたデザインワークショップを行っている。ベルリン在住
なんか、眠れなくなってきました。(^_^;)
図にしてみました。
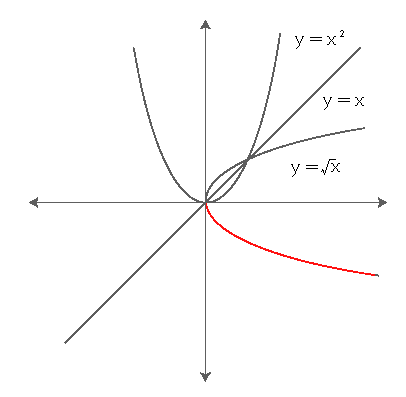
増分の話は、接線の角度の変化、つまり微分すれば解けそうですね。
y=(xの二乗)とy=√xが似てますね。そりゃそうです。y=√xってことは、(yの二乗)=xってことですものね。y=(xの二乗)を90度回転、あるいはy=xに対して対象の図形です。ということは、(xのn乗根)と、(xのn乗)が対応するということです。0<=xのn乗根<1 ですから0から1の間に1から∞が対応しているわけです。
y=(xの二乗)でy軸より左があるのは、マイナスの数の2乗はプラスだということですね。それではそれを回転したときの√xのx軸より下の部分(赤い部分)は何でしょう。√をつけるとマイナスになる数?ι(二乗して−1になる数)ではありませんよ。そんな数はない。ないというか、作ればいいんですよね。それとももうあるのかな。
高校の数学、あんなに好きだったのにすっかり忘れてしまいました。数学は「役に立たない機械」?