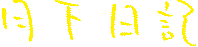Book-off 220 yen including tax
This is a book that I had no particular intention of buying. My child came home for New Year's holiday, and I went to Book-off by myself to kill time. Apparently he bought something, but at that time he said, ``Even though I said I would use my points, they didn't deduct the points,'' so I went to Book-off with him. Since the points were for a limited time, I went with the intention of having them deducted. I happened to find this book, and I thought it would be less troublesome to buy this book with points than to get a refund, so I paid my child 220 yen and used the points (lol).
By chance, at that time, I was reading "[What is the theory of quantum gravity]?" (https://nomado.moo.jp/medias/2024/01/09/post-4054/) by Kaoru Takeuchi. , Bluebacks) and was thinking about the space-time continuum. That book had a lot of formulas for Bluebacks, and I couldn't understand them at all.
The fact that spacetime has the smallest unit means that spacetime is not continuous and cannot be infinitely divided.
Formula
b = a + 1 (b is one more than a)
If a is "1", then b is "2". A can contain any number (unless there is a condition). 1, 2, 3, 1/2, √2, π... For now, let's consider "natural numbers (1, 2, 3...)". For "1, 2, 3", b becomes "2, 3, 4". If you make a bigger and bigger, you will get one more number than that, but can a be made infinitely large? It's actually (naturally) impossible. Even if you think of a big number, there is another number (b) that is one bigger.
Does this expression represent something "impossible"? No, it is actually possible to say "give me an apple" or "give me another apple" (the question of whether or not you will receive it or whether there is one more remains, but you can say "please") .
Set (collection)
A collection (set) of numbers "1, 2, 3..." that can be put in a, and a number "2, 3, 4" that can be put in b. Which one is more common? Since there is no "1" in b, it seems that b has "one less". Let's count. What should I do to count? How do you compare whether there are the same number of apples and oranges (which one has more)? When comparing red balls and white balls at a sports festival, you take them out of the basket one by one, and the one that remains wins (has the most).
Now, let's take it out. "Red 1 - White 2", "Red 2 - White 3", "Red 3 - White 4", etc. it will not finish. After all, there are an infinite number of natural numbers. But you can make predictions. Is the same. This is because for every (element of) a, there is one b, that is, (a + 1).
Now let's consider "b = a ✕ 2". While a is "1, 2, 3...", b is "2, 4, 6...". b is an even number. Natural numbers are made up of (positive) even numbers (2, 4, 6...) and odd numbers (1, 3, 5...). If you compare a natural number with an even number, is the even number half the number? No, just like before, one a corresponds to one b, so it's the same.
Now let's consider b = 1 ÷ a. a is "1, 2, 3, 4..." while b is "1, 1/2 (0.5), 1/3 (0.3333...), 1/4 (0.25)... ·"is. It can also be said that one cake is divided by a number of people. The maximum value of b is 1, and as a increases, b decreases (approaches zero). Of course, b is only 1 as a natural number, and the others are not natural numbers, but the numbers are still the same (one a and one b).
A "number line" represents numbers by the location of the line (distance from the origin). It can be said to be a ``spatialization'' to visualize numbers. The natural number a continues at regular intervals until eternity. When viewed from 1, b (1 ÷ a) approaches 0 as the interval gets closer and closer, but it never exceeds 0.
This is one of "Zeno's paradoxes": "If something is flying, it will not fly (it will stay still)".
We have talked about the "size", "quantity", "many" and "few" of infinite numbers, but in set theory this is called "cardinality". The cardinality of natural numbers and the cardinality of odd and even numbers are the same. Cantor expressed this with the symbol ``ℵ0 (Aleph Null)''. You can predict that the cardinality of numbers that can be expressed as fractions (rational numbers) is aleph null. So, is the number line completely filled with rational numbers? no. "√2" and "π" cannot be expressed as a fraction. These are called "irrational numbers."
Do irrational numbers "exist" (exist)? For example, √2 is the diagonal of a square with side 1. π is the length of the circumference of a circle with a diameter of 1. If ``1'' for a side or diameter is ``existed,'' then it would be better to say that √2 and π also ``exist.'' The combination of rational numbers and irrational numbers is called "real numbers." In fact, it might be better to say that real numbers that are not rational numbers are called irrational numbers. The thing to keep in mind here is that √2, π, and e (also called Napier's number, Napier's number, Napier's number, Euler's number; the base of natural logarithms) are ``human-given meanings.'' In that sense, the natural numbers are the same. An even number is a number that is divisible by 2, and an odd number is a number that is not divisible by 2. It's also true that 7 is a "lucky number". The study of finding meaning in numbers is called "gematria (numerology)" (p. 37).
Continuous
Now, are all the points on the number line filled with real numbers (continuous)? My image is that when you pick up a number line with your fingers and lift it up, either it connects smoothly and lifts up, or it snaps apart.
Cantor defined the cardinality of real numbers as "ℵ1". This means that it is "continuous". Then, we defined
2ℵ0 = ℵ1 (2 to the power of an integer/rational number is an irrational number)
. In other words, "all numbers on the number line are expressed as decimals." The number of decimal digits is ℵ0. Between ℵ0 and ℵ1, ℵ1 is "more concentrated", but there is no in between. This is called the "continuum hypothesis." But this is no longer a problem if you put it another way.
All real numbers are called real numbers. A number line is a spatial representation of real numbers. (My definition)
However, this does not mean that ``the number line is continuous'' or ``numbers other than real numbers do not exist.'' This becomes the question, "Are there any numbers other than a few?"
Each decimal digit is a natural number (1, 2, 3, 4, 5, 6, 7, 8, 9, 0 in decimal system, 0, 1 in binary system) . A real number is a set of infinite combinations of natural numbers (this is the meaning of "2ℵ0"). In other words, real numbers cannot be separated from "physical reality."
Imaginary numbers
There are no imaginary numbers in this book. An imaginary number is an imaginary number. I've never used or seen imaginary numbers. I can't even imagine it. So, I will not dwell on it.
If there is a number that cannot be represented by a decimal number, the continuum hypothesis breaks down. However, even if it is a ``non-existent'' or ``imaginary'' number, it is not an imaginary number. Rather, an imaginary number can be defined as "i = √-1". In other words, it is a ``meaningful'' or ``human-given'' number. If we say "no," then "zero" and "negative numbers (minus numbers)" will also mean "no."
Russell's Paradox
"I'm telling a lie." Is what I'm saying true or false? If it's true, I'm lying, so it's false; if it's false, I'm telling the truth, so it's true.
Suppose we consider a set (S(x)) of things (elements, say x) that satisfy a certain condition (S). In the previous example, if the condition is "something that is divisible by 2", the set of things (elements) that satisfy that condition will be S(x) = {2,4,6,...}. However, the set of conditions ``x is not an element of x'' is self-contradictory. This is because I don't know (can't decide) whether x is an element or not (I cut it short).
Russell's paradox means that there is no universal set (a set that contains everything). (P.191)
Russell's paradox clearly showed that in mathematics, you can't get anything by cutting a blank line. It is not enough to define a set by saying, ``This is a set.'' We must create a set whose elements actually exist. In the same way, just because we define a unicorn does not prove that unicorns exist. (ibid.)
Cantor's final legacy was the realization that there can be no all-inclusive set (Russell's paradox also shows this). The reason there cannot be an all-inclusive set is that for any set, there is always a larger set (specifically, a power set, which consists of all subsets of the original set). ). (P.197)
Just saying “There is a number line that represents the points of all real numbers” does not prove that such a line exists. not.
If you consider that there is no universal set called the largest matryoshka, and if you think about the absolute that can never be reached, you can also understand Gödel's incompleteness theorem. Isn't that what it feels like? This is because it asserts that there is always something outside the system we are in, something bigger than the given system. (P.205-206)
However, as long as you are operating within that document, you cannot delete that document. To delete the document (or move it to another file), you must exit the document and perform the operation within the larger system.
There are concepts and properties that cannot be grasped from within a given system, and in order to understand them, one must move to a higher level. On the other hand, as Cantor showed, there is no highest level, so there will always be ideas and properties within any system that cannot be grasped. An analogy to this would be that humans will never be able to understand God. No matter what kind of system the human mind is, there are things that cannot be fully understood within that finite system. Since God is of a higher order than humans, it is impossible for the finite human mind to understand God. (P.206)
Finally, we have come to the conclusion that there is no such thing as a "whole". If this is the case, what humans can always recognize is "parts." What humans always recognize is a part of existence, and they cannot recognize the ``whole existence'', that is, ``existence itself.''
Is the human mind finite? I don't understand. The idea is that even if the human mind is infinite, something higher exists. Could it be God? Is that god ℵ1 or ℵℵ? And is there no intermediate existence between humans and God? I do not know. "Humans will never be able to understand God."
I don't even know if it was correct to define "real number" as ℵ1 in the first place. Even if that is a "definition," I don't know if it has been proven that it exists. In the end, the question ``Is the number line continuous?'' is ``If the real number is ℵ1, the number line is the visualization of it, and it is continuous. The only thing I could understand was that it was a definition (axiom) of "saying that there is". This definition is the ``continuum hypothesis,'' and it has nothing to do with other areas of mathematics.
Cohen completed the remaining half of the journey that Gödel left unfinished. Cohen's proof made it conclusively clear that the validity of Cantor's continuum hypothesis cannot be proven within the currently used axiomatic system of set theory. (P.221)
The continuum hypothesis was completely independent of the axiom system of set theory (ZF + selection axiom). Whether the continuum hypothesis is true or false, it is impossible to prove or disprove it within the current axiomatic system. The selection axiom was shown to be independent from the ZF axiom system. (P.223)
I don't understand it, but that's what it seems like.
What is the sum of "🍎🍎🍎 (3 apples)" and "🍊🍊🍊 (3 oranges)"? "3+3=6", but that is neither "six apples" nor "six oranges". If I had to say it, it would be ``6 fruits.'' At this time, there is a transition to a superordinate concept. A superordinate concept can also be referred to as ``from a species to a class'' or ``from a part to a whole.'' In fact, not every apple or tangerine is the same. There are only "individual objects". 3 and 6 are not inherent in individual objects, but are merely "concepts" separate from individual objects.
“If you understand the individual (parts), you can understand the whole” This is reductionism (Wiki, Kinji Imanishi “Nature/Humanity/Civilization What Cantor demonstrated was not the proof of God, but the impossibility of proving God, and the failure of reductionism.
Number/Counting
As long as you start from a finite number (be it five or 500 trillion), any mathematical operation (addition, information, exponential operation) ) cannot reach the first infinite cardinal number. The first infinite cardinal number ℵ0 is "unreachable" from finite cardinal numbers (ordinary numbers, in short). However, once we reach the first infinite base ℵ0, we can create higher-order infinite bases by exponentiation. (P.226)
Is infinity just an assumption? I wonder why each digit is a natural number even though it is an infinite decimal (for example, 1.2354789484125... ). The ``number'' of each digit is made from a range that I can understand. Calling "🍎🍎🍎" "three apples" is a human decision. Even though we are called humans, we only have a limited range (culture). I think that "three apples" and "three apples" have different meanings. I don't even know if "تفاحة" means apple.
In the first place, there are many cultures where there is no (or almost no) concept of "number" (Caleb Everett's "[The Invention of Numbers]" (https://nomado.moo.jp/medias /2023/12/13/post-4051/)” Misuzu Shobo, reference). Numbers are certainly useful. But that's because we live in a culture where numbers are convenient (necessary). An example of this is money (such as 1,000 yen or 10,000 yen). In countries that require money, it is necessary to know numbers. Imagine a world without money. When do you use large numbers in everyday life? Only one house can be lived in at a time. One glass of water, one pair of chopsticks, one bowl, one cup of rice...you don't need that many. More than that, I think there are very few situations where we are conscious of numbers. When I drink water, I don't think, ``Right now, I have 15cc in my mouth.'' I probably don't usually realize that I have two arms, or that I have five fingers.
When something we have is gone, we are very conscious of it. It is very inconvenient when one of your arms is injured (even if you don't lose it). But that doesn't mean you always think, ``I wish I had three eyes.'' I think the question ``Is the number line continuous?'' leads to the question ``Why do we count?'' and ``There is a number 3'' is just a rule (theorem, hypothesis). Is it not?
According to Cantor, physical reality does depend on mathematical principles. If so, continuums, numbers, and their properties should be reflected (FF) in various aspects of physical reality. But Cantor also adds: But mathematics does not need the physical world to justify its existence. (P.235-236)
Whether you think so or not depends on each person. Indeed, numbers are useful. However, I feel that the author is forgetting that the culture in which he lives is one that requires numbers. Just saying ``numbers are real,'' ``infinity exists,'' or ``God exists'' does not prove that things ``exist'' in the same way that unicorns do.
Thinking about infinity
Many mathematicians and philosophers appear in this book. The central character is Cantor. As he grappled with infinity, he became depressed.
Almost recovered from his first attack in 1884, Cantor set his sights on one goal and devoted his time to the study of English history and literature. The goal is to prove that Francis Bacon is the true author of Shakespeare's plays. (P.169)
Another important figure, Gödel, was
Cantor spent many years trying to prove that Shakespeare was not the author of Shakespeare's plays. However, Gödel sought to prove that Leibniz had created a theory that was probably not his own. (P.217)
Hmm, it's dangerous. In addition, the book contains many anecdotes about many people, making it a very interesting read.
I'm not good at math (or arithmetic), but when I read this book and tried to imagine what it would be like, my mental state became unstable. I can't understand what I can't visualize, and I don't think I have. The calculation ``3 + 3 = 6'' and the formula `` b = a + 1'' are more than ``understood'' or ``remembered.'' If you remember it, you will get a good score on the test. I learned it just for that purpose, and I don't know if I could visualize it. I never thought, ``Why does that happen?'' and if you ask such questions, you will be called a ``stupid child'' or a ``troublesome child.'' You may be taken to the hospital and given an "intelligence test." This is because we live in a society where it is inconvenient (or difficult or impossible to live) if you do not understand that if you buy something that costs 800 yen for 1,000 yen, you will receive 200 yen in change.
Recently, I have been thinking of reconsidering what I have learned and what I take for granted, but I have come to realize that this is impossible. However, I always try to keep in mind that ``That's not the case,'' ``That's not necessarily the case,'' and ``There may be societies where this isn't the case.''
Quantum Mechanics
Now, regarding the ``quantum theory of gravity'' that led me to read this book, according to it, there is a minimum unit of time and space.
This is basically a question of what the natural length and weight are in the geometric unit system. As will be seen in Chapter 3, in the geometric unit system, length ``1'' is the Planck length of approximately 10-33 cm, and weight ``1'' is the Planck weight of approximately 10-8 kg. become. (Previously cited “What is quantum gravity theory”, P.28)
< p>In quantum mechanics, energy and the position of elementary particles are expressed as probabilities. If the orbit (location) of an electron is represented by a model, it will look like a single orbit (left) for a particle, and if it is represented by the level of probability, it will look like the one on the right.

Quantum is more like a ``thing'' (or a phenomenon) than a ``thing''. (Ibid., p. 8)
It is a probability that a certain particle exists at a certain place with a certain energy. Having said that, the length and time we perceive are immeasurably large, so the apple in front of our eyes never disappears in reality. The fact that there is a minimum unit means that it is not continuous, whether or not there is a gap in unit time or unit space is another matter. However, although it is not written in the previous paper, time and space may also be expressed as particles of probability in the same way as electrons. As shown in the picture above.
Space is a "field" that has a certain amount of energy. In Aristotle's terms, it is a container for matter (energy). However, I think that there is no distinction between the container and the contents. "Space is a field that has energy, size, and time in a stochastic manner." They are like clouds of electrons, intermingled with each other. Its location and time can be confirmed ``after the fact'' by observation. I can't do it, but someone please put it into an equation.
When we think of time and space (time and space) in this way, there is no point in thinking about "continuity". A certain unit of spacetime may be here or there. Well, you could say it's everywhere at the same time. The ordering is just for convenience.
"There are three apples here. From the right, they look sweet, they look sour, and they look rotten." It's easy to understand that "left and right" was something humans thought up for convenience. In fact, there are many cultures where there is no "left and right." ``Sweet and spicy'' are also cultural differences. ``Whether or not something is rotten or not'' is also a cultural question (there are many ways to judge whether something is rotten or not). Judging whether or not the apple is "alive" is also culturally dependent. In that case, wouldn't it be better to say that "3" is also cultural?
Numbers are real. And I think that its reality has nothing to do with humans. (P.233)
If the continuum did not exist, could the approach of calculus based on the continuum be so effective? (P.234)
According to Cantor, physical reality does depend on mathematical principles. If so, continuums, numbers, and their properties should be reflected (FF) in various aspects of physical reality. But Cantor also adds: But mathematics does not need the physical world to justify its existence. (P.235-236)
``Numbers are real'' is a cultural/historical thing, just like ``God is real.'' The validity of calculus and set theory is cultural and historical, just like the necessity of numbers. Because we live in such a society. If you live on a deserted island or in the depths of a jungle, calculus will be useless (meaningless).
I would like to take Cantor's words as directly telling us about the "culture and historicity of numbers."