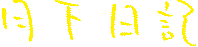1 + 1 = 2
I saw "Proof of 1 + 1 = 2" in "Yobinori". It uses Peano's axioms (the specific content of the proof is omitted).
Therefore, I thought that "1" and "2" are symbols rather than numbers. Certainly, if you write it in kanji, it will be "Ichi" and "II". It's a symbol, isn't it? Therefore, it can be either "△" or "×".
For some reason, only 0 (zero) is defined ("0" is a natural number).
In fact, 0 is also a symbol. It can be "zero", "oh", or "maru". You can also use "★".
What is zero? I feel like "nothing". "There are zero cats in my house." Means "there are no cats in my house **", right?
Therefore, zero is "denial". What does it mean that zero "exists"?
By the way, there was a book I hadn't read because I wanted to read it. This is the book "Discovery of Zero".
Structure of this manual
The first half is "Discovery of Zero-Origin of Arabic Numbers-" and the second half is "Cut a Straight Line-Continuous Problem-".
It's not history of mathematics. It depicts the relationship between mathematics, culture, and society.
Abacus
It starts with the story of the abacus, which is familiar to us and is gradually disappearing. In other words, it's a scale story. Abacus was also used in Europe. In the abacus, the place where the ball (pearl) is not moving is "0".
In decimal, 10 numbers can represent all natural numbers
"South Africa's Bushman numerals are limited to one and two, and then there is only the word" many "." (P.18) Since folklore and anthropology are changing, this knowledge is now available. I don't know if it is correct. Unnecessary knowledge is not transmitted, so the way the society should be will determine how to count.
How many have you actually counted? One sheep, two sheep, three sheep ... For example, I think many people have seen a wad of 100 million yen, but few actually counted it. I think very few people have 100 million yen. Who needs the numbers "100 million" and "1 trillion" for what? Think about the number you need (the number you can count) in your daily life. I think there aren't many "4 family members" or "5 ballpoint pens". Even if you have 5 (or 100) boll point pens, you can actually use only one at a time. Even if you think "no matter how many bodies you have," you actually have only one body.
The number we can feel (use) is by no means large. I have three 6T (tera) hard disks. 1 tera is 1,000,000,000,000, but since it is not a countable number, we have "3" "things" called "6 tera hard disks", and in reality we only use the numbers "6" and "3". It will be. [1] [2]
There is a ", (comma)" between the numbers, because in Europe and the United States, "thousands" are grouped together. Then, the "thousands" become a "unit" and the "thousands" are combined into the next mass. You cannot walk 100 million yen with a 1-yen coin. A 10,000-yen bill is a collection of 10,000. I was scoring every 4 digits in China and Japan.
Long division and paper
The decline of the abacus is due to the rise of long division (not the calculator), which requires a large amount of paper. Paper is an integral part of printing technology. The relationship with the Renaissance, the Reformation, the Age of Discovery, etc. is described. Mathematics does not develop (change) by itself, but various conditions influence it.
This is the great thing about this book, which describes mathematics from a historical and social perspective, rather than looking at it in the framework of mathematics.
Decimals and fractions
It's the second half. The story goes on, and it's about decimals and fractions. From the story of recurring decimals to the story of infinite series.
Just by changing the position of the parentheses of the infinite series, it becomes 0 or 1. "It is said that some mathematicians were happy to shed tears, saying that they could understand the news that was made from all things. (LF) From now on, it's just humorous. There is nothing else, but he was still serious, though there may be other stories like this, not just in mathematics, and in the olden days. It seems like I can't cut it. ”(P.71) The author's humor and irony, but he seems to be talking about me (laughs).
Continuous-infinite
In the second half, we will move on to the discussion of rational numbers and irrational numbers. And to the story of "Zeno of Elea".
"By the way, the monetary system started as a result of the colonial development of the Greeks and the large-scale commercial transactions between cities on the Mediterranean coast, and this system also made Ionia. It gradually spread to the mainland of Greece. ”(P.94) It's a little subtle. But there is no doubt that the monetary system started with commercial transactions.
"From the Greek point of view, letters were merely a tool of record, and were thought to have no power like" spoken words "as a means of communicating thoughts and knowledge. That is, "written words are merely images of living and living words, merely shadow masters", and the lively and true knowledge answers questions, refutes, and corrects misunderstandings (FF). It is said that this can only be conveyed by a method of discourse with spoken words, such as to prevent omissions. (LF) When considering the superiority and inferiority of school education and distance learning ... ”(P.95-96)
This theory becomes clear when considering the difference between Socrates and Plato. Socrates just stuck to the question and answer (dialogue). But Plato was a character enthusiast. ("Socrates's defense")
Plato may have had the opposite idea rather than being different from Socrates. Is it "Great Mind Plato" or "Weirdo or Transformer Plato"?
Here, the author takes up "Aspects of Greek Genius" ("Aspects of Rare Genius", later "Aspects of Greek Spirit") by S. Ech Butcher (1850-1910).
This book "Some Aspects of the Greek Genius" has a translation by Tetsuro Watsuji and Hidenaka Tanaka, but it seems to be in the old font. I want to read ...
It seems to be full of interesting things such as ideographic characters (ideographic characters) and phonetic characters, the divergence between characters and art, and the attitude of a rare spirit toward the law.
"The Greeks thought that mathematicians-for example, theorems in Euclidean geometry-already existed before mathematicians discovered them, whereas in modern times It can be said that the mathematical facts, as Poancare said, are believed to be "mathematicians-sometimes the whims of mathematicians create this." (P.105) This is a transformation of the view of nature itself. ("How do you see nature now?")
The story of the Pythagorean cult. Socrates "contrary to the Sophist, he sought to establish an objective concept of good. It is said that Socrates himself was not interested in mathematics itself, but Socrates gives a definition to the concept-that is, The advocacy of what each concept is, its essence, and its content-has had a great influence on the subsequent methods of mathematics. "(P.145)
It seems that I understood the mathematical explanation after this, and I did not understand (^ _ ^;).
Discovery of Zero
Regarding the discovery of Zero, it only states objective matters. I think that such a statement is also preferable.
"There is zero." The existence of nothing means that "there is nothing that does not exist" and "there is nothing that does not exist". There seems to be room to think (although it seems confusing) before taking it for granted.
It seems that the ancient Greeks thought that "nature hates vacuum". It is passed on to Christianity through Hellenistic period. [3]
The idea that "there is nothing" and "everything is present" gives rise to the ideas of "acknowledge what should not be" and "make what should not be without". Either way, it's cramped that there is only "yes" or "affirmation" in the world.
I think it is important to recognize different forms and different societies. I do not think that "there is something that is not there", but that "there is nothing that is not there" and "denial is not the denial of existence, but denial is the way it is."
Finish reading
This book was written in 1939. It's more than 80 years ago. History (archeology) seems to have changed with various discoveries since then. However, I think the ideas and methodologies that this book adheres to are still important. It is a famous book.
<書抜>
武見太郎氏にささぐ
はしがき
昭和十四年夏 札幌にて 吉田洋一
改版に際して
昭和三十一年十一月 池袋にて 吉田洋一
再改版に際して
昭和五十三年十二月十八日 浦和にて 吉田洋一
零の発見 アラビア数字の由来
一
二
三
(サラセン帝国)「この帝国はその後まもなく東西二つのカリフ国に分裂したが、両王朝とも歴代の教王(カリフ)が保護奨励につとめたので、学問芸術とも大いに興り、その二つの首都バグダッド(メソポタミア)とコルドバ(スペイン)とは当時の文化の二大中心たるの観を呈するにいたった。」(P.7)
四
「この例からみても、八世紀の終わりから十一世紀にかけては、明治以来われわれが英語その他の西欧語を学んできたと同じ意味において、アラビア語の習得が知識にいたる唯一の鍵であった、というのも、あながちに、誇張の言とのみしりぞけられないであろうと思われる。」(P.8)
五
六
七
八
九
「かくして零の発見、単なる記号としてばかりでなく、数としての零の認識、続いては、この新しい零という「数」を用いてする計算の発明、これらの事業を成就するためには、けっきょくインド人の天才にまたなければならなかったのであった。」(P.20)
一〇
一一
「代数学がギリシャで発達になかったことについては、さきにものべたギリシャ数字の影響も無視することはできないが、ある意味で、きわめて具体的であって、代数学のような形式的方面には向かなかったということも、その理由として考えられているのである。」(P.24)
一二
一三
一四
「このようにゆくたてがあったとはいえ、しばらくの間は、スペインのキリスト教とはイスラム教徒からきわめて寛大なとりあつかいをうけて、信教の自由も許され、また官職につく途さえも彼らにはとざされない状態にあった。」(P.29)
一五
一六
一七
一八
一九
二〇
「たとえば、当時の医学においては、男の肋骨の数は女より一本少ないというのが定説になっていた、ということを想起してみるのも一興であると思う。」(P.49)
「すなわち、聖書の権威の前には、手でさわって数えてみる手数だけでただちにわかるような簡単な事実さえ、問題にならないという時代なのであった。」(P.49)
二一
「古くからつづいていたキリスト教との聖地巡礼は、ついに、十一世紀にいたって、新たに勃興したセルジュク・トルコ族のパレスチナ占領にあって、にわかにその道をとざされてしまった。これに対抗して十一世紀末から十三世紀末にかけて、数回にわたって、もよおされた十字軍の遠征は、一時的な成功はえながらも、結局のところ、その目的たる聖地回復の業をなしとげられずに終わった。」(P.50)
「数学史にピサのレオナルド、もしくは、フィボナチの名前で知られている数学者はピサの全盛時代といわれる十二世紀の後半に商人の子として生まれた。」(P.50)
「こうした比較研究の結果でもあろうか、レオナルドはピサに変えるや一二〇二年 Liber Abaci (ソロバンの書)とよばれる一書を著して、インド記数法ならびにこれによる商業算術をはじめて組織的にイタリアに紹介したのであった。」(P.51)
二二
二三
二四
「この製紙術が高麗の僧雲徴によって日本に伝えられたのは、人のよく知るように、推古天皇の御代(六一〇年)であるが、これが西の世界に広まったのは、これよりずっと後のことであった。」(P.57)
二五
三二
計算尺
三三
「自然科学がほしいままな仮説から演繹される空論の体系であった状態から脱皮して、ようやく自然の観察・測定を重んずる実証科学に成長していったのは、このころからのことなのである。ケプラーやガリレオはネイピアやビュルギとほぼ同時代であるし、「自分は仮説をこしらえない」と叫んだニュートンの出現も、対数の発見以後そう長くを経ないころのことであったことは記憶しておいてもよいことであろう。」(P.83)
「ところが、この傾向も十六世紀に至ってようやく変調を示しはじめ、十七世紀にはいると、偉大な数学者の多くはアルプスの北から輩出するようになって来た。」(P.84)
三四
「この計算尺・電卓・コンピュータの進歩によって、西欧においても、筆算のおこなわれる機会はしだいに少なくなってきている。かつては、その筆算に対する機能の故に、かっくもヨーロッパに普及するにいたったアラビア数字も、かくしてその「計算数字」としての役割は、ようやく狭められていくように見える。しかしながら、単に「記録数字」としてだけにしても、位取り記数法に立ちまさった記数法を考えることは困難なのであって、この記数法は今後とも永くその生命をたもっていくことであろうと思われる。」(P.86)
直線を切る 連続の問題
四
(ブチャー『ギリシャ天才の諸相』)「エジプト人がその記念建造物に使った記号は単に音の符牒ではなくて、そのあらわす対象物の模像であった。もしギリシャ人がエジプト人のように観念を象徴する文字の術を作り上げていったならば、書くことは話すことと同じく、芸術の一種となり、した(FF)がって尊敬されたであろう。」(P.96-87)__十二世紀に、文字は模像ではなく、観念を象徴するものになる。
(つづき)「しかしギリシャ人に書き物を疑惑視させた原因は、彼らの芸術的本能のみではなかった。行為においても彼らは法式の前にたじろいだ。不変の規則は行為を硬化させる。屈伸自在に弾力的なこと、不断に調整することの必要は強く感ぜられた。法律に対するギリシャ精神の態度は顕著な適例である。たいていの東洋民族は書かれた宗教法典を持っており、それは直接に神の心かまたは手からきたと想像され、特殊の神聖さを与えられた。しかしギリシャ人においては書物は決して宗教的な聖化を受けなかった。」(P.98)
七
「いいかえれば、ギリシャ人のとった純学問的な論理的方法とても、これまた、数学に対する一つの態度にすぎなかった、というべきであろうというのである。さらに一歩を進めて、前節に述べたバビロニアの数学に関する推測が、もし、正しいとすれば、この民族の数学はエジプト人の実用数学とギリシャ人の理(FF)論的数学との間に介在するまた別の一つの方であるともいうことができるであろう。」(P.104-105)
八
「(略)きわめて大ざっぱないいあらわし方をすれば、ギリシャ人は、数学的事実 たとえば、ユークリッド幾何学における諸定理 は数学者がこれを発見するに先だって、すでにそれ自身存在するものと考えていた、これに反して、現代では、数学的事実は、ポアンカレのいったように、「数学者自身が 時として数学者の気まぐれがこれを創造する」のであると考えられている、ということができるであろう。」(P.105)__論理はあらかじめ存在するか。神の手から人の手に。
一一
「天体の軌道が円であるとされたのも、また、円が曲線中のもっとも完全なものという考えから出たものであった。」(P.113)
二四
「ソフィストのなかの第一人者プロタゴラス(紀元前四八〇−四一一年)の「あることについても、無いことについても人間が万物の尺度である」という有名な言葉が示すごとく、ソフィストは認識の主観性を説き、絶対的真理を否定し、進んで、倫理・国法なども相対的価値を有するにすぎない、と考えたのであった。」(P.144)
「彼はソフィストのためにあやまられた青年たちをみちびいて、よき市民たらしめんとし、ソフィストに反して、客観的な善の概念を確立しようとつとめたのであった。ソクラテス自身は数学そのものには興味をもたなかったといわれるが、ソクラテスが概念に定義を与えること すなわち、それぞれの概念が何であるかということ、その本質、その内容を述べること を唱導したことは、以後の数学の方法に多大の影響を与えずにはいなかった。たとえば、ユークリッドの『原論』が、開巻劈頭、点や直線等の定義からはじまるのも、この影響の現れであるといっていえないことはないであろう。」(P.145)
「これが𝔄1に属するならば、これは𝔄1の右端にあるわけで、𝔄2には左端がないことにある。またこれが𝔄2に属すればこれは𝔄2の左端にあたり、𝔄1には右端がないことになろう。デデキントはこのことを指して連続性の本質である、といおうというのである。いいかえれば、直線が連続であるというのは、𝔄1に右端あり𝔄2にも左端ありということもなければ、また𝔄1に右端なく𝔄2にも左端なしということも決してないことを意味するというのである。」(P.166)